কেন্দ্রীয় প্রবণতার পরিমাপ (Measures of Central Tendency)
কেন্দ্রীয় প্রবণতার পরিমাপ এমন পরিসংখ্যানগত মান যা ডেটার মধ্যে "কেন্দ্র" বা "মধ্যবিন্দু" নির্দেশ করে। এটি ডেটার সাধারণ বা বৈশিষ্ট্যগত মান নির্ধারণে সহায়ক। কেন্দ্রীয় প্রবণতার পরিমাপের মাধ্যমে আমরা ডেটাসেটের মধ্যম মান বা প্রতীকী মান খুঁজে পাই, যা ডেটার সাধারণ বৈশিষ্ট্য বোঝাতে সাহায্য করে।
কেন্দ্রীয় প্রবণতার পরিমাপের প্রধান তিনটি পদ্ধতি রয়েছে:
গড় হল একটি ডেটাসেটের সব মানের যোগফল বিভক্ত করে ডেটাসেটের মোট উপাদানের সংখ্যা দিয়ে।
গণনা পদ্ধতি:
গড় = ΣΧ/ N
এখানে,
• ∑X = সব ডেটার যোগফল
N = ডেটার মোট সংখ্যা
উদাহরণ:
ডেটাসেট: ৪, ৫, ৭, ৮, ৯
গড় = 4+5+7+8+9 = = ৬.৬
মাধ্যমিক মান একটি ডেটাসেটের মধ্যম মান, অর্থাৎ, যেটি ডেটাসেটের সব মানের মধ্যে মাঝখানে অবস্থান করে। যখন ডেটাগুলি ছোট থেকে বড় বা বড় থেকে ছোট পর্যন্ত সাজানো হয়, তখন কেন্দ্রীয় মান হলো মধ্যের মান।
গণনা পদ্ধতি:
উদাহরণ:
ডেটাসেট: ৪, ৫, ৭, ৮, ৯
মাধ্যমিক মান = ৭ (কারণ এটি মধ্যের মান)
মোড হল একটি ডেটাসেটে সবচেয়ে বেশি বার ঘটে এমন মান। এটি ডেটাসেটের শ্রেণী বা শ্রেণীগত বৈশিষ্ট্য নির্ধারণ করতে ব্যবহৃত হয়।
গণনা পদ্ধতি:
ডেটাসেটে যেই মানটি সবচেয়ে বেশি আসে, সেটি হল মোড।
উদাহরণ:
ডেটাসেট: ৪, ৫, ৫, ৭, ৭, ৮
মোড = ৫, ৭ (কারণ ৫ এবং ৭, উভয়ই সবচেয়ে বেশি সংখ্যা হয়েছে)
পাঁচজন ছাত্রের দৈনিক নাস্তা বাবদ খরচ যথাক্রমে 20, 50, 70, 80, 130 টাকা।
দুইটি ধনাত্মক সংখ্যার গাণিতিক গড় 25 এবং জ্যামিতিক গড় 20।
কেন্দ্রীয় প্রবণতা হলো একটি ডেটাসেটের কেন্দ্রীয় মান বা ডেটার সাধারণ বৈশিষ্ট্য প্রকাশ করার জন্য ব্যবহৃত একটি পরিমাপ। এটি মূলত ডেটাসেটের চারিত্রিক বৈশিষ্ট্য বোঝানোর জন্য ব্যবহৃত হয়।
ডেটা বিশ্লেষণের ক্ষেত্রে, কেন্দ্রীয় প্রবণতা তিনটি সাধারণ পদ্ধতিতে প্রকাশ করা হয়:
১. গড় (Mean):
গড় হলো একটি ডেটাসেটের সকল মানের যোগফলকে ডেটার মোট সংখ্যা দ্বারা ভাগ করার মাধ্যমে প্রাপ্ত পরিমাপ।
গড়ের সূত্র:

যেখানে,

উদাহরণ:

২. মধ্যক (Median):
মধ্যক হলো একটি ডেটাসেটের মধ্যবর্তী মান, যা ডেটাগুলোকে ক্রমাগত সাজানোর পরে পাওয়া যায়।
উদাহরণ:
ডেটাসেট: 3, 8, 10, 12, 15
মধ্যক: ১০ (মধ্যবর্তী মান)
ডেটাসেট: 4, 6, 9, 11
মধ্যক:
![]()
৩. বহুলক (Mode):
বহুলক হলো একটি ডেটাসেটে সবচেয়ে বেশি বার পুনরাবৃত্ত মান।
উদাহরণ:
ডেটাসেট: 2, 3, 4, 4, 6, 6, 6, 8
বহুলক: 6 (সবচেয়ে বেশি বার দেখা যায়)
কেন্দ্রীয় প্রবণতার পরিমাপ আমাদের ডেটাসেটের সাধারণ বৈশিষ্ট্য সম্পর্কে ধারণা দেয়। গড়, মধ্যক এবং বহুলক এই তিনটি পদ্ধতি বিভিন্ন পরিস্থিতিতে ডেটা বিশ্লেষণের জন্য কার্যকরী।
কেন্দ্রীয় প্রবণতার পরিমাপগুলি (Measures of Central Tendency) হলো এমন পরিসংখ্যানিক পরিমাপ যা একটি ডেটাসেটের কেন্দ্রীয় বা সাধারণ মান নির্দেশ করে। এটি ডেটাসেটের প্রধান বৈশিষ্ট্যগুলো বুঝতে সাহায্য করে এবং সাধারণত তিনটি গুরুত্বপূর্ণ পরিমাপ অন্তর্ভুক্ত করে:
গড় হলো ডেটাসেটের সব মানের যোগফলকে ডেটাসেটের মানের মোট সংখ্যায় ভাগ করে পাওয়া মান। এটি ডেটাসেটের কেন্দ্রীয় মানের একটি গুরুত্বপূর্ণ নির্দেশক।
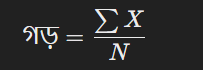
গণনা পদ্ধতি:
যেখানে:
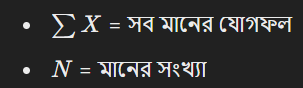
উদাহরণ:
ডেটাসেট: 5, 10, 15
গড়:
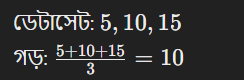
মধ্যক হলো ডেটাসেটের ক্রমানুসারে সাজানো মানগুলোর মধ্যে কেন্দ্রে থাকা মান। যদি ডেটাসেটের মোট মান বিজোড় হয়, তবে মধ্যক হবে একক একটি মান; আর জোড় হলে মাঝখানের দুইটি মানের গড় হবে মধ্যক।
উদাহরণ:
ডেটাসেট (বিজোড়): 3, 5, 7
মধ্যক: 5
ডেটাসেট (জোড়): 2, 4, 6, 8
মধ্যক:
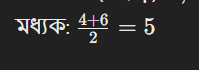
বহুলক হলো ডেটাসেটের মধ্যে সবচেয়ে বেশি সংখ্যক বার পুনরাবৃত্তি হওয়া মান। এটি বিশেষত সেই ক্ষেত্রে গুরুত্বপূর্ণ যেখানে ডেটাসেটের মধ্যে কিছু নির্দিষ্ট মান বেশি ঘটে।
উদাহরণ:
ডেটাসেট:2, 3, 3, 5, 7
বহুলক: 3
১. ডেটার সারাংশ দেওয়া: ডেটাসেটের মোট প্রবণতা বোঝায়।
২. তুলনামূলক বিশ্লেষণ: বিভিন্ন ডেটাসেটের মধ্যে তুলনা করতে সাহায্য করে।
৩. বিশ্লেষণ সহজ করা: গবেষণা ও পরিসংখ্যানে ডেটার বিশ্লেষণ সহজতর হয়।
কেন্দ্রীয় প্রবণতার পরিমাপ গড়, মধ্যক এবং বহুলকের মাধ্যমে ডেটাসেটের মৌলিক বৈশিষ্ট্য নির্ধারণ করতে সাহায্য করে। প্রতিটি পরিমাপ ভিন্ন ভিন্ন পরিস্থিতিতে কার্যকর।
একটি আদর্শ গড়ের জন্য কিছু গুরুত্বপূর্ণ গুণাবলী রয়েছে যা গড়কে নির্ভুল, কার্যকর এবং ব্যবহারযোগ্য করে তোলে। আদর্শ গড়ের প্রয়োজনীয় গুণাবলী হলো:
গড় এমন হতে হবে যা সহজে বোঝা যায় এবং গণনা করা সহজ হয়, যাতে এটি যে কেউ ব্যবহার করতে পারে।
গড় এমনভাবে নির্ধারণ করা উচিত যা প্রদত্ত ডেটার প্রকৃত কেন্দ্রীয় অবস্থান প্রকাশ করে। এটি ডেটার প্রকৃতি এবং বন্টন সম্পর্কে স্পষ্ট ধারণা দেয়।
গড় এমন পদ্ধতিতে নির্ধারণ করা উচিত যাতে এটি সবসময় একই ফলাফল দেয়। এটি নির্ভরযোগ্য হতে হবে।
গড়কে এমন হতে হবে যা ডেটার প্রতিটি মানকে বিবেচনায় নেয়। এতে ডেটার কোনো মান অগ্রাহ্য হওয়া উচিত নয়।
গড়কে এমন হতে হবে যা বাস্তব সংখ্যা দিয়ে প্রকাশ করা যায়। এটি ডেটার প্রকৃতি অনুযায়ী প্রাসঙ্গিক হতে হবে।
আদর্শ গড় এমন হতে হবে যা এক বা একাধিক অত্যধিক বড় বা ছোট মানের কারণে বিকৃত না হয়।
গড় পরিসংখ্যানের অন্যান্য সূচকের সাথে সঙ্গতিপূর্ণ হতে হবে এবং তাদের সাথে কার্যকর সম্পর্ক বজায় রাখতে হবে।
গড়কে এমনভাবে গণনা করা উচিত যা বিভিন্ন ক্ষেত্র এবং বিভিন্ন পরিস্থিতিতে কার্যকরভাবে ব্যবহার করা যায়।
গড় একই এককে প্রকাশ করতে হবে যেমনটি ডেটা সংগ্রহ করা হয়েছে। এককের পরিবর্তন গড়ের মানকে প্রভাবিত করবে না।
গড় এমন হওয়া উচিত যা বিভিন্ন ধরনের পরিসংখ্যান বিশ্লেষণে ব্যবহার করা যায় এবং প্রয়োজনে উপযুক্ত সংস্করণে সামঞ্জস্য করা যায়। যেমন: গাণিতিক গড়, মধ্যমা, বা মোড ইত্যাদি।
এই গুণাবলী নিশ্চিত করে একটি গড় পরিসংখ্যান বিশ্লেষণে কার্যকর ভূমিকা পালন করতে পারে।
কেন্দ্রীয় প্রবণতা পরিমাপগুলোর সাহায্যে ডেটাসেটের গড় বা কেন্দ্রীয় মানটি নির্ধারণ করা হয়। সাধারণত তিনটি প্রধান কেন্দ্রীয় প্রবণতা পরিমাপ ব্যবহার করা হয়: গড় (Mean), মধ্যক (Median), এবং মোড (Mode)। এদের মধ্যে পার্থক্য এবং বৈশিষ্ট্যগুলো নিচে আলোচনা করা হলো:
সংজ্ঞা:
ডেটাসেটের সমস্ত উপাত্তের যোগফলকে উপাত্তের সংখ্যা দিয়ে ভাগ করে গড় নির্ণয় করা হয়।
উদাহরণ:
ডেটাসেট: ২, ৪, ৬, ৮, ১০
গড় = (২ + ৪ + ৬ + ৮ + ১০) / ৫ = ৬
বৈশিষ্ট্য:
সংজ্ঞা:
ডেটাসেটকে ক্রমানুসারে সাজানোর পর মাঝের উপাত্তটি মধ্যক।
উদাহরণ:
ডেটাসেট: ২, ৪, ৬, ৮, ১০
মধ্যক = ৬ (মাঝের উপাত্ত)
ডেটাসেট (সমান সংখ্যক উপাত্ত): ২, ৪, ৬, ৮
মধ্যক = (৪ + ৬) / ২ = ৫
বৈশিষ্ট্য:
সংজ্ঞা:
ডেটাসেটের মধ্যে যে উপাত্তটি সবচেয়ে বেশি বার উপস্থিত, সেটি মোড।
উদাহরণ:
ডেটাসেট: ২, ৪, ৬, ৬, ৮
মোড = ৬ (সবচেয়ে বেশি বার উপস্থিত)
বৈশিষ্ট্য:
| বৈশিষ্ট্য | গড় (Mean) | মধ্যক (Median) | মোড (Mode) |
|---|---|---|---|
| উপযোগিতা | সমজাতীয় ডেটাসেট | বিচ্যুতিমূলক ডেটাসেট | ঘন পুনরাবৃত্তির ক্ষেত্রে |
| সংবেদনশীলতা | চরম মান দ্বারা প্রভাবিত | চরম মান দ্বারা প্রভাবিত নয় | চরম মান দ্বারা প্রভাবিত নয় |
| প্রকৃতি | পরিমাণগত | ক্রমানুসারে ভিত্তিক | গুণগত ও পরিমাণগত |
| গাণিতিক ব্যবহার | সহজে ব্যবহারযোগ্য | তুলনামূলকভাবে কম | গাণিতিকভাবে সীমিত |
গড়, মধ্যক এবং মোড কেন্দ্রীয় প্রবণতা পরিমাপের গুরুত্বপূর্ণ অংশ। গড় একটি নির্দিষ্ট গাণিতিক মূল্য দেয়, মধ্যক চরম মান এড়াতে সাহায্য করে এবং মোড ডেটাসেটে ঘন পুনরাবৃত্তি খুঁজে বের করে। ডেটার প্রকৃতি এবং প্রয়োজন অনুযায়ী এই তিনটি পরিমাপের ব্যবহার নির্ভর করে।
১. সহজ ও সরল উপস্থাপনা
২. ডেটার প্রতিনিধিত্ব করে
৩. পরিসংখ্যান বিশ্লেষণে ব্যবহারযোগ্য
৪. তুলনা করার সুবিধা
৫. ব্যবহারিক প্রয়োগ
১. প্রতিনিধিত্বের সীমাবদ্ধতা
২. চরম মানের প্রভাব (গড়ের ক্ষেত্রে)
৩. তথ্যের অসম্পূর্ণতা
৪. অযৌক্তিক ফলাফল
৫. সব ধরনের ডেটার জন্য প্রযোজ্য নয়
কেন্দ্রীয় প্রবণতার পরিমাপগুলো পরিসংখ্যান বিশ্লেষণের ক্ষেত্রে গুরুত্বপূর্ণ, তবে এর সীমাবদ্ধতা সম্পর্কে সচেতন থাকা জরুরি। সঠিক পদ্ধতি নির্বাচন নির্ভর করে ডেটার প্রকৃতি এবং গবেষণার লক্ষ্য নির্ধারণের উপর।
গাণিতিক গড় একটি গুরুত্বপূর্ণ কেন্দ্রীয় প্রবণতার পরিমাপ। এর বিভিন্ন বৈশিষ্ট্য বা ধর্ম রয়েছে, যা ডেটাসেট বিশ্লেষণের সময় গুরুত্বপূর্ণ ভূমিকা পালন করে। নিচে গাণিতিক গড়ের প্রধান বৈশিষ্ট্যগুলো দেওয়া হলো:
গাণিতিক গড় সহজে গণনা করা যায়। ডেটাসেটের সকল মানের যোগফলকে ডেটার মোট সংখ্যার দ্বারা ভাগ করলেই গড় পাওয়া যায়।
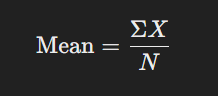
ডেটাসেটের মধ্যে কোনো চরম মান থাকলে গড় তার প্রভাব বহন করে। উদাহরণস্বরূপ, যদি কোনো ডেটাসেটে একটি অত্যন্ত বড় বা ছোট মান থাকে, তাহলে গড় তার দিকে ঝুঁকে পড়ে।
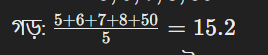
উদাহরণ:
ডেটাসেট: 5, 6, 7, 8, 50
গড়:
(৫০ এর কারণে গড় উচ্চতর হয়েছে।)
গাণিতিক গড় প্রতিটি মানকে অন্তর্ভুক্ত করে, ফলে এটি পুরো ডেটাসেটের প্রতিনিধিত্ব করে।
গড় একটি একক মান হিসেবে ডেটাসেটকে উপস্থাপন করে, যা ডেটাসেটের সার্বিক বৈশিষ্ট্য নির্দেশ করে।
গাণিতিক গড় বিভিন্ন বৈজ্ঞানিক এবং পরিসংখ্যানিক বিশ্লেষণে ব্যবহার করা হয়। এটি অন্যান্য পরিমাপের সাথে সহজেই সমন্বয় করা যায়।
ডেটাসেটে নতুন কোনো মান যোগ বা বিয়োগ করলে গড় তাৎক্ষণিকভাবে পরিবর্তিত হয়।
![]()
উদাহরণ:
ডেটাসেট: 10, 20, 30
গড়:
নতুন মান 40 যোগ করলে:
গড়:
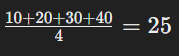
যদি ডেটার মান বিভাজক বা দশমিকের মাধ্যমে আসে, গড় প্রায়শই দশমিক আকারে থাকতে পারে।
যদি একটি ডেটাসেট একাধিক উপগোষ্ঠীতে বিভক্ত হয়, তাহলে পুরো ডেটাসেটের গড় হলো উপগোষ্ঠীগুলোর গড়ের সমষ্টি।
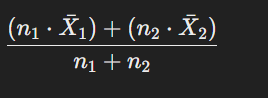
যেখানে,

গাণিতিক গড় মানের যোগফলের বণ্টিত পরিমাণ নির্দেশ করে এবং এটি সরল বণ্টনের ক্ষেত্রে কার্যকর।
গাণিতিক গড় একটি গুরুত্বপূর্ণ পরিসংখ্যানিক মাপকাঠি যা ডেটাসেটের সার্বিক বৈশিষ্ট্য নির্দেশ করে। তবে এটি চরম মানের প্রতি সংবেদনশীল এবং সব পরিস্থিতিতে ব্যবহার উপযোগী নয়। সঠিক বিশ্লেষণের জন্য গাণিতিক গড়ের সীমাবদ্ধতাগুলো বোঝা প্রয়োজন।
ভার আরোপিত গড় এমন একটি গড়ের প্রকার যেখানে ডেটাসেটের প্রতিটি মানের জন্য একটি নির্দিষ্ট গুরুত্ব বা ওজন (Weight) দেওয়া হয়। এই পদ্ধতিতে প্রতিটি মানকে তার ওজন দিয়ে গুণ করে এবং তারপরে গুণফলগুলোর যোগফলকে ওজনের মোট যোগফলে ভাগ করে গড় নির্ধারণ করা হয়।
ভার আরোপিত গড় গণনার সূত্র হলো:

যেখানে:

ধরা যাক, একটি শিক্ষার্থীর তিনটি পরীক্ষায় প্রাপ্ত নম্বর 80, 90, এবং 70 । পরীক্ষাগুলোর ওজন যথাক্রমে 2, 3, এবং 5 । এখন ভার আরোপিত গড় বের করা যাক:
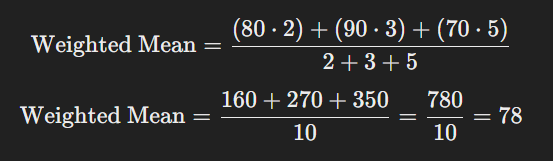
অতএব, গড় স্কোর হলো 78 ।
ভার আরোপিত গড় এমন পরিস্থিতিতে প্রয়োজন যেখানে ডেটাসেটের বিভিন্ন মানের প্রভাব বা গুরুত্ব সমান নয়। এটি বিভিন্ন ক্ষেত্রে ব্যবহৃত হয়, যেমন:
১. প্রতিটি মানের গুরুত্ব বিবেচনা করে সঠিক গড় বের করা যায়।
২. বিভিন্ন প্রেক্ষাপটে কার্যকর, যেখানে সাধারণ গড় ব্যবহার করা অসম্ভব বা অপ্রাসঙ্গিক।
৩. বাস্তব সমস্যা সমাধানে আরও নির্ভুল ফলাফল প্রদান করে।
ভার আরোপিত গড় একটি বিশেষ পদ্ধতি যা ডেটাসেটের প্রতিটি মানের গুরুত্ব বা প্রভাব অনুযায়ী গড় নির্ধারণ করে। এটি বিভিন্ন ক্ষেত্রে, যেমন শিক্ষাব্যবস্থা, ব্যবসা, অর্থনীতি এবং গবেষণায়, ব্যবহারিক সমস্যার সমাধানে অত্যন্ত প্রয়োজনীয়।
বিভাজক মানসমূহ (Divisors) হল এমন সংখ্যাগুলোর সেট, যেগুলি একটি নির্দিষ্ট সংখ্যাকে ভাগ করতে পারে কোনো অবশিষ্টাংশ ছাড়া।
উদাহরণ:
ধরা যাক, 12 সংখ্যার বিভাজকগুলো খুঁজে বের করতে হবে।
12 কে যেসব সংখ্যা অবশিষ্টাংশ ছাড়া ভাগ করতে পারে, সেগুলো হলো:
1, 2, 3, 4, 6, 12।
এখানে,
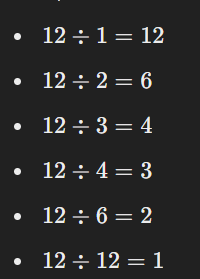
তাহলে, 12 এর বিভাজক মানসমূহ হল: 1, 2, 3, 4, 6, এবং 12।
বিভাজক মান গণিতের বিভিন্ন ক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে, যেমন:
Read more